Michaelis-Menten Models with Constant Harvesting of Restricted Prey Populations Minimum Place and Amount Capacity
DOI:
https://doi.org/10.15642/mantik.2021.7.2.107-114Keywords:
Food chain model, Michaelis-Menten model, Prey-predator modelAbstract
Food chain modeling is currently developing rapidly. The ecosystem is protected from the chain of eating and eating processes. All living things need each other, but if the process of eating them is not balanced, then the extinction of living things will occur. One of them is the prey and predator model that serves as a balancer in the food chain system. The Michaelis-Menten model is a prey-predator model that essentially prevents prey extinction. The problem is how to keep the prey from becoming extinct but with maximum harvesting in one place and the minimum amount of prey at the right time. The method used to overcome this problem is to add two new variables to the Michaelis-Menten model, namely the minimum number of prey and the capacity of the place to be occupied. It is seen that the system will be in equilibrium if the predator mortality rate is large so that the prey is kept from extinction until harvesting. In addition, the right time for good breeding can also be determined. From this model, it is found that the right time for harvesting so that prey extinction does not occur is
Downloads
References
S. O. Lehtinen, “Ecological and evolutionary consequences of predator-prey role reversal: Allee effect and catastrophic predator extinction,” J. Theor. Biol., vol. 510, p. 110542, 2021, DOI: 10.1016/j.jtbi.2020.110542.
X. Dongmei and J. Leslie Stephen, “Bifurcation Of A Ratio Dependent Predator-Prey System With Constant Rate Harvesting,” vol. 65, no. 3, pp. 737–753, 2013.
A. Mapunda, E. Mureithi, N. Shaban, and T. Sagamiko, “Effects of Over-Harvesting and Drought on a Predator-Prey System with Optimal Control,” Open J. Ecol., vol. 08, no. 08, pp. 459–482, 2018, doi: 10.4236/oje.2018.88028.
H. Shim, T. Operations, and S. Korea, “Visualization and Interaction Design for Ecosystem Modeling Introduction Background Lotka-Volterra Model and Textual Modeling Two-Dimensional System Dynamics Modeling Three-Dimensional Integrative Modeling Summary Further Reading,” pp. 3685–3693, 2008.
S. Marom, “Pembentukan Model Mangsa Pemangsa Dengan Pemanenan Mangsa,” vol. 1, no. 2, pp. 181–187, 2013.
A. Anas, “Model Pemangsa dan Mangsa lotka Voltera Proporsional terhadap Model Logistik Von Bertallanfy Termodifikasi,” Al-Fitrah, vol. 12, pp. 101–116, 2017.
T. Henny M, U. R. Heri Selistyo, and W. Widowati, “Model Pertumbuhan Logistik Dengan Waktu Tunda,” J. Mat., vol. 11, pp. 43–51, 2008.
A. Tsoularis and J. Wallace, “Analysis of logistic growth models,” Math. Biosci., vol. 179, no. 1, pp. 21–55, 2002, doi: 10.1016/S0025-5564(02)00096-2.
D. Xiao and S. Ruan, “Global dynamics of a ratio-dependent predator-prey system,” vol. 290, no. 10071027, pp. 268–290, 2001.
M. Robert, Worldwide Differential Equations with Linear Algebra. Worldwide Center of Mathematics, LLC, 2012.
A. Keng Ceng, Differential Equations: Models and Methods. McGraw-Hill Education, 2005.
C. H. Edwards and D. E. Penney, Elementary Differential Equation.
H. Anton and C. Rorres, Elementary Linear Algebra with Applications. John Wiley & Sons, INC., 2005.
J. Stewart, Calculus. Thomson Learning, Inc, 2008.
T. PNV, Dynamical System, An Introduction with Application in Economics and Biology. Springer- Verlag. Heidelberg, Germany, 1994.
Downloads
Published
How to Cite
Issue
Section
License
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work

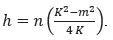






.png)




